VKSU UG Semester-1 Physics | what is derivative?

by

what is derivative?

A derivative is a fundamental concept in calculus that represents the rate of change of a function with respect to its independent variable. It’s a central tool in mathematics, extensively used in various fields such as physics, engineering, economics, and more recently in machine learning and data science. Understanding derivatives is crucial for analyzing how quantities change over time or in response to other variables.

Introduction to Derivatives

Derivatives are essentially the slope of a function at a specific point, indicating how the function behaves locally. They allow us to examine the instantaneous rate of change of a function, capturing the precise moment-by-moment variation rather than an average over an interval. This concept was developed to solve problems involving motion, but its applications extend far beyond physics into virtually every branch of science and engineering.

Historical Development

The notion of derivatives can be traced back to the work of ancient mathematicians like Archimedes, who used geometric methods to find areas and tangents to curves. However, it was Isaac Newton and Gottfried Wilhelm Leibniz who formalized the modern calculus concepts in the 17th century. They independently developed the calculus of infinitesimals, which laid the foundation for differential calculus and integral calculus.

Formal Definition and Notation

Formal Definition and Notation

Interpretation and Applications

  1. Rate of Change: Derivatives measure how a function changes with respect to its input variable. For example, in physics, velocity is the derivative of position with respect to time, and acceleration is the derivative of velocity.
  2. Optimization: Derivatives help in finding maximum and minimum values of functions. Critical points, where the derivative is zero or undefined, indicate potential extremes.
  3. Graphical Behavior: They provide insights into the shape and behavior of functions. Concavity, inflection points, and curvature can be analyzed using second derivatives.
  4. Integral Calculus: Derivatives are closely related to integrals through the Fundamental Theorem of Calculus, which connects the rate of change (derivative) and the accumulation (integral) of a quantity.

Differentiation Rules

The process of finding derivatives involves applying various rules and techniques, including:

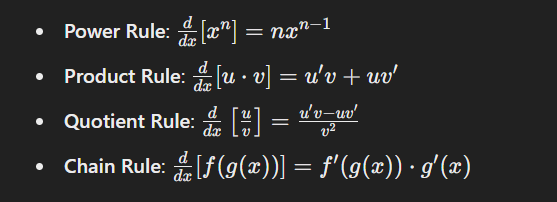
Differentiation Rules

These rules allow derivatives to be computed for complex functions composed of simpler parts.

Advanced Concepts

  1. Higher Order Derivatives: Derivatives of derivatives, such as acceleration (second derivative of position) or jerk (third derivative).
  2. Partial Derivatives: Extending derivatives to functions of several variables, crucial in multivariable calculus and fields like physics and economics.
  3. Implicit Differentiation: Applying differentiation to equations where the dependent variable is not explicitly expressed as a function of the independent variable.
  4. Applications in Science and Engineering: From modeling physical phenomena to optimizing algorithms, derivatives are indispensable in solving real-world problems.

Conclusion

Derivatives are fundamental to understanding change and variation in mathematical models across diverse disciplines. They provide a precise mathematical tool for analyzing rates of change, optimization problems, and the behavior of functions. As technology advances, the applications of derivatives continue to expand, making them an essential concept in both theoretical mathematics and practical applications.

In summary, derivatives form the cornerstone of calculus, enabling us to grasp the dynamics of continuous change in the natural and human-made worlds with unparalleled precision and insight.

Post Views: 110

Leave a Comment